分析并查集的时间复杂度

并查集的时间复杂度

其实自从高二开始学习并查集就发现这个数据结构真的奇妙，能解决许多问题，但是对时间复杂度就不太理解，大二退役之后我开始想去知道为什么是这个奇妙的时间复杂度，遂有此文。

本文参考了：OI-Wiki，coursera上的算法课程

这里证明并没有引入势能分析，但是相关东西异曲同工。

引入

并查集是一种用于管理元素所属集合的数据结构，实现为一个森林，其中每棵树表示一个集合，树中的节点表示对应集合中的元素。

并查集支持两种操作：

• 合并（Union）：合并两个元素所属集合（合并对应的树）
• 查询（Find）：查询某个元素所属集合（查询对应的树的根节点），这可以用于判断两个元素是否属于同一集合

朴素算法

查询：我们需要沿着树向上移动，直至找到根节点。

合并：要合并两棵树，我们只需要将一棵树的根节点连到另一棵树的根节点。

那么这样的时间复杂度有多少呢？

排名（Rank）

对于并查集的中的每个树，其中 $V$ 是节点集合，$E$ 是边集合，$r$ 为树的叶节点，对于任意节点 $v \in V$，定义节点 $v$ 的排名 $\text{rank}$ 为：

• 如果 $v$ 没有叶节点 ，则 $\text{rank}(v) = 0$
• 如果 $v$ 有叶节点 ，则 $\text{rank}(v) = \max{\text{rank}(\text{son})} + 1$

某个节点到根结点的路径上的边数的最大值为排名（Rank）

注意：下面所有秩都和 $\text{rank}$ 一个意思

那么就有以下性质：

1. 对于任意节点 $x$，$\text{rank}(x)$ 只会增加
2. 在合并时，只有根节点的 $\text{rank}(x)$ 才有可能增加
3. 在一条路径（从下至上）中 $\text{rank}(x)$ 严格递增

rank 的引理 1

对于任意的查询Find操作，该操作中生成的图 $G$，$|G| = n$，对于所有的 $r \in {1,2,3 \dots n}$，$\text{rank} = r$ 的元素个数 $\leq \frac{n}{2^r}$

证明引理 1

1. 假设一：如果两个的不相同的点的 $\text{rank}$ 相同，那么他们的子树不可能有重合部分。

   • 反证：如果有重合部分，那么一定有一个路径 $x\to z \to y$，$z$ 为重合部分，$x,y$ 为两个 rank 相同的点，那么可以得出 $x$ 和 $y$ 之间有更大的祖先，那么就有更大的 $\text{rank}$，与假设不符。

2. 假设二：$\text{rank}=x$ 的子树的元素 $\ge 2^n$（数学归纳法）

证明：Base：$\text{rank} = 0,size =0$

inductive step：

1. 不一样的子树大小，$\text{rank}$ 不变

2. 一样的子树大小， $\text{rank} + 1$

$X_s = 合并前一个子树的大小 \geq 2^r,Y_s = 合并前另一个子树的大小 \geq 2^r$

合并后，Union(x,y)得到了新祖先 $Z$，$\text{rank}(z) = r+1$

$Z_s \geq 2^r + 2^r \geq 2^{r+1}$，假设二证明完毕

现在我们来证明引理 1：n 个元素，我们设每个 $\text{rank}=x$ 的子树的大小为 $x$，假设二可知，$x \geq 2^r$

我们两边取倒数，并且同时乘一个 n，那么可以得出 $\dfrac{n}{x} \leq \dfrac{n}{2^r}$，那么可以看出左边就是 $\text{rank} = r$ 的元素个数，引理 1 也证明完毕了。

时间复杂度

证明了这么多，我们也能看出来 $\text{rank}$ 其实就是一个子树的深度，也是我们最多要查询的次数。

首先，$最大\text{rank}的个数=祖先的个数=1$，显然，那么根据引理1，得出：

$$1 \leq \frac{n}{2^r} \ \Rightarrow 2^r \leq n \Rightarrow r \leq \log_{2}n$$

那么我们可以得到查询和合并的时间复杂度为 $O(\log_{2} n)$

路径压缩+启发式合并（按秩合并）

上面的朴素算法已经很快了，但是考虑一种可能，如果这个不是一个正常的树，而是一条链，而我们正常的去查询最底下的节点，那么复杂度将会退化成 $O(n)$，这并不是我们想要的，想到我们查询时有许多地方时冗余的，我们就想到了路径压缩。

路径压缩：查询过程中经过的每个元素都属于该集合，我们可以将其直接连到根节点以加快后续查询。

在合并时我们又想到了这两个的 $\text{rank}$ 不同也会导致路径压缩的时候会多了一些不该有的操作。

启发式合并（按秩合并）：合并时，选择哪棵树的根节点作为新树的根节点会影响未来操作的复杂度。我们可以将节点较少或深度较小的树连到另一棵，以免发生退化。

另一种做法则是使用“秩”来比较树的大小。”秩“的定义如下：

• 只有根节点的树（即只有一个元素的集合），秩为0；
• 当两棵秩不同的树合并后，新的树的秩为原来两棵树的秩的较大者；
• 当两棵秩相同的树合并后，新的树的秩为原来的树的秩加一。

容易发现，在没有路径压缩优化时，树的秩等于树的深度减一。在有路径压缩优化时，树的秩仍然能反映出树的深度和大小。在合并时根据两棵树的秩的大小，决定新的根节点，这被称作按秩合并。

Theorem

注意：经过路径压缩过时，$\text{rank}$ 不变，相当于被冻结了，不管压缩到哪都不会改变

内容：通过“按秩合并”和“路径压缩”优化后，进行 $m$ 次合并+查询的操作的时间复杂度为 $O(m \log^ n)$，其中 $\log^ n$ 表示对 $n$ 反复应用对数运算，直到结果小于等于 1 所需要的次数，一般叫迭代对数。

$x$	$\lg^* x$
$(−\infty, 1]$	$0$
$(1, 2]$	$1$
$(2, 4]$	$2$
$(4, 16]$	$3$
$(16, 65536]$	$4$
$(65536, 2^{65536}]$	$5$

证明

首先我们来定义一个 $\text{rank\, blocks}$（秩块）；${0},{1},{2,3,4},{5,\dots, 2 4 },{17,18,\dots,2^{16}},
{65537,\dots,2^{65536}},\dots,{\dots,n}$

很显然这些块只会有 $O(\log^* n)$ 个。

我们给每个节点分类，我们现在称一个节点 $x$（可变）是好的当：

1. $x$ 或者 $x$ 的父节点为根节点
2. 父亲的 $\text{rank}$ 比自己的 $\text{rank}$ 大。 注意：$\text{rank} 不变$

如果两个条件都不符合，那么就是坏节点。

我们会尽量将一个节点变成好节点。

第一个要点：要点：每次查找操作只会访问 $O(\log^ n)$ 个好节点 （计算方式为 $2 + 秩块的数量 = O(\log^ n)$）

结论：在 $m$ 次操作中完成的总工作量可以表示为两种：

• $O(m \log^* n)$（访问好节点的次数）
• 访问坏节点的总次数，下面就来论证。

首先我们思考，在路径压缩中，其父节点被更改为具有严格更大 $\text{rank}$ 的节点，这种情况最多只会发生 $2^k$ 次，之后 $x$ 将永久成为“好节点”。（很显然，在路径压缩中，那个节点相当于在往上跳，最多跳到这个 block 的第一个）

总时间复杂度：$O(m \log^* n) + O(访问坏节点的次数)$。

我们对一个秩块 ${k+1, k+2, \dots, 2^k}$ 分析：

对于每个最终秩处于此块的 $x$，当 $x$ 是“坏节点”时的访问次数最多为 $2^k$。

具有最终 $\text{rank}$ 处于此块的对象总数为：

$$\sum_{i=k+1}^{2^k} \frac{n}{2^i} \leq \frac{n}{2^k}$$

因此，此秩块中对“坏节点”的访问总次数最多为 $n$。

因为只有 $O(\log^* n)$ 个秩块。

总时间复杂度：

$O((m + n) \log^ n)$，在正常操作中 $m$ 与 $n$ 同阶，就可以是 $O(m \log^ n)$，证明完毕。

Tarjan’s Bound

该证明在1975年由Tarjan完成，后在1989年，由Fredman证明该结构下无法找到更好的时间复杂度

内容：通过“按秩合并”和“路径压缩”优化后，进行 $m$ 次合并和查找操作的时间复杂度为 $O(m \alpha(n))$，其中 $\alpha(n)$ 是反阿克曼函数。

阿克曼函数

需要两个自然数作为输入值，输出一个自然数，它的输出值增长速度非常高。

定义：

$$A(m,n) = \begin{cases}n + 1 & \text{如果 m=0} \\ A(m-1,1) & \text{如果 m>0 且 n=0} \\ A(m-1,A(m,n-1)) & \text{如果 m>0 且 n>0 }\end{cases}$$

由于这个函数的增加速率非常快，那么它的反函数就相应的增长的非常慢。

反函数的定义：对于每个 $n \geq 4$，$\alpha(n)$ 是满足 $A_k(2) \geq n$ 的最小 $k$ 值，其中 $A_k(2)$ 是阿克曼函数。

$\alpha(n) = 1 \Rightarrow n=4$

$\alpha(n) = 2 \Rightarrow n=5 \dots 8$

$\alpha(n) = 3 \Rightarrow n=9 ,10\dots 2048$

$\alpha(n) = 4 \Rightarrow n=4\dots n(n 满足 \log^*n= 2048)$

$\cdots$

证明

我们定义 $x$ 为不是根节点 $\delta(x)$ 是最大的 $k$ 使得 $\text{rank}(\text{parent}[x]) \geq A_k(\text{rank}(x))$

显然， $\delta(x)$ 是递增的。

这里有一个性质：只要 $\text{rank} \geq 2$ 的点，那么一定会有 $\delta(x) \leq \alpha(n)$

证明：

$$A_{\alpha(n)}(2) \geq n \geq \text{rank}(parent[x]) \geq A_k(\text{rank}(x))$$

其中 $n \geq \text{rank}(parent[x])$ 很显然一定成立，左边其实就是上面反函数的定义，右边就是 $\delta(x)$ 的定义，最左边与最右边分别进行反函数，即证成立。

这里我们继续定义好节点与坏节点：

一个点为好的节点当且仅当符合下面几个条件，我们称这个节点为坏节点：

1. $x$ 不是根节点
2. 它的父亲不是根节点
3. $\text{rank}(x) \geq 2$
4. $x$ 存在祖先 $y$ 使得 $\delta(y) = \delta(x)$

否则，$x$ 是好的节点。

同 Hopcroft-Ullman 类似，在一次路径中最多有 $\Theta(\alpha(n)) \leq 2 +2 +\alpha(n)$ 个好节点。

那么最终 $m$ 次操作（合并与查询）的总时间复杂度：$O(m\alpha(n))(访问好节点的次数)+访问坏节点的次数$

下面我们来计算一下这个坏节点的个数，我们同样只先看一次路径的：

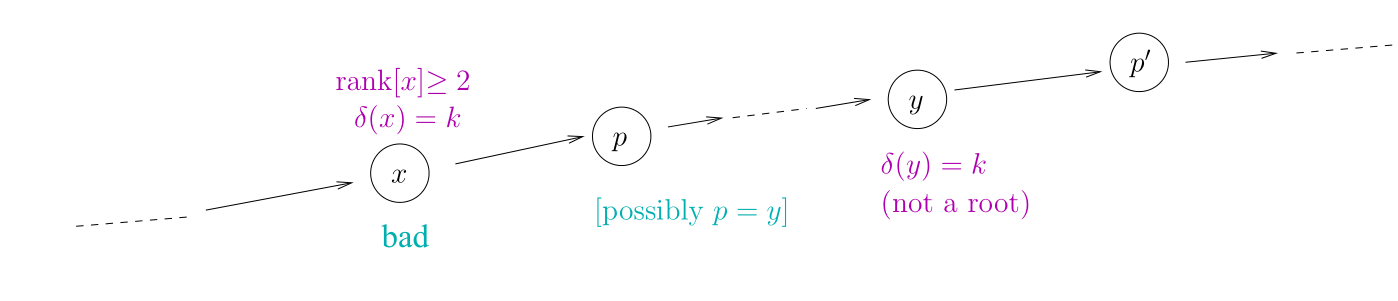
路径压缩：$p’$ 是 $x$ 的新父亲或者更向上，则有：

$$\text{rank}(x的新父亲) \geq \text{rank}(p') \geq A_k(\text{rank}(y)) \geq A_k(\text{rank}(p))$$

中间这个过渡我们用到了上面 $\delta(x)$ 的定义，其他的都很显然。

假设 $r = \text{rank}(x)$，然后我们对 $x$ 做 $r$ 次查找（路径压缩），假设每次都是有用的，那么我的 $\delta(x)$ 至少 $+1$

为什么？我们不从理性的（数学的）角度去分析，而是去从感性的角度，首先想 $\text{rank}(x) = 0，1$，显然根据定义，本身就是好节点，成立。

那么 $\text{rank}(x) \geq 2$ 呢？压缩一次会压缩到好节点的同地方，下一次必然会压缩到下一个 $\delta(x) + 1$ 中，所以的证，而且是至少。

那最多可以加多少次 1 呢？$\alpha(n)$ 次

那么 $x$ 是坏的 $\leq r \alpha(n)$

那么我们开始算总共访问坏节点的次数：

$$\begin{align*} &总共访问坏节点的次数 \\ &\leq \Sigma_{所有节点}\text{rank}(x) \cdot \alpha(n) \tag 1\\ &= \alpha(n) \cdot \Sigma_{r \geq 0} \,r \,(\text{rank}=r 节点的个数) \tag2\\ &\leq n \alpha(n) \Sigma_{r \geq 0} \frac{r}{2^r} \tag 3\\ &= O(n \alpha(n)) \end{align*}$$

我们来解释一下这个东西怎么来的，在 $(2) \to (3)$ 中的推导中我们用到了 rank 的引理 1，不理解的可以倒回去看看，这里我们对每个 $r$ 都用了一个引理 1 并相加，$(3)$ 中的 $\Sigma_{r \geq 0} \frac{r}{2^r}$，其实是个几何级数，最后是个常数，可以省略，就得到了坏节点的次数。

那么我们能得出总共的时间复杂度为：

$O((n+m) \alpha(n))$，同样在正常操作中 $m$ 与 $n$ 同阶，就可以是 $O(m \alpha(n))$，证明完毕。