堆排序(Heapsort)
堆排序(Heapsort)
堆排序指利用堆数据结构所设计的一种排序算法,
排序
首先建立大顶堆,然后将堆顶的元素取出,作为最大值,与数组尾部的元素交换,并维持残余堆的性质;
之后将堆顶的元素取出,作为次大值,与数组倒数第二位元素交换,并维持残余堆的性质;
以此类推,在第 $n-1$ 次操作后,整个数组就完成了排序。
- 如何从一个无序序列建成一个堆?
- 如何将堆顶的元素取出之后,调整剩余元素成为一个新的堆?
下面是具体步骤:
先解决第一个问题,首先现将数组从上至下转换成二叉树,对于一个节点 $i$,它的父节点为 $i/2$,左儿子为 $2 \times i$,右儿子为 $2 \times i + 1$。
现在是无序堆,我们要让这个无序堆变成最大堆(最小堆)。
从最后一个子堆开始,首先开始对比左右儿子,有的话取较大的子节点,再与父节点相比,如果比父节点大,那么就将儿子与父亲交换,这样一个子堆就变成了最大堆。
最后自顶向上去创建最大堆,直至最大堆完成。
将创建完成的最大堆的父节点给下放,放到最下面的一个节点,不动它了,之后对前面的继续变成最大堆,不断重复这些步骤。
例子
首先我们选一个数组 [100, 5, 3, 11, 33, 6, 8, 7],按照数组顺序来构建一棵树。如下图
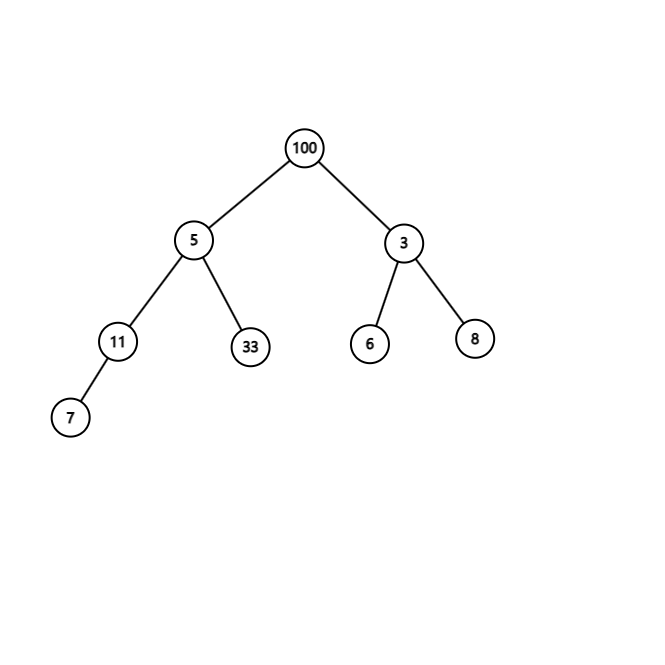
按照步骤,先看最后一个子堆,就是最下面的 11,发现 11 没有右儿子,有个左儿子 7,符合最大堆的性质,现在在看以 5 为父节点的堆,发现右儿子更大,再与父节点比较,发现儿子比父节点大,那么 5 和 33 交换,交换后子堆符合最大堆的性质。
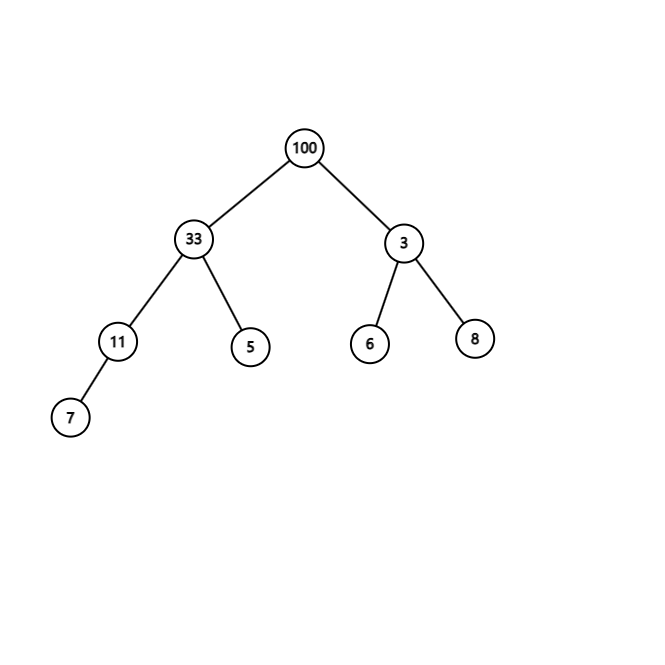
再按照上面的规则将 3 的堆,变成最大堆,再将 100 为父节点的堆变成最大堆,最后成为下图:
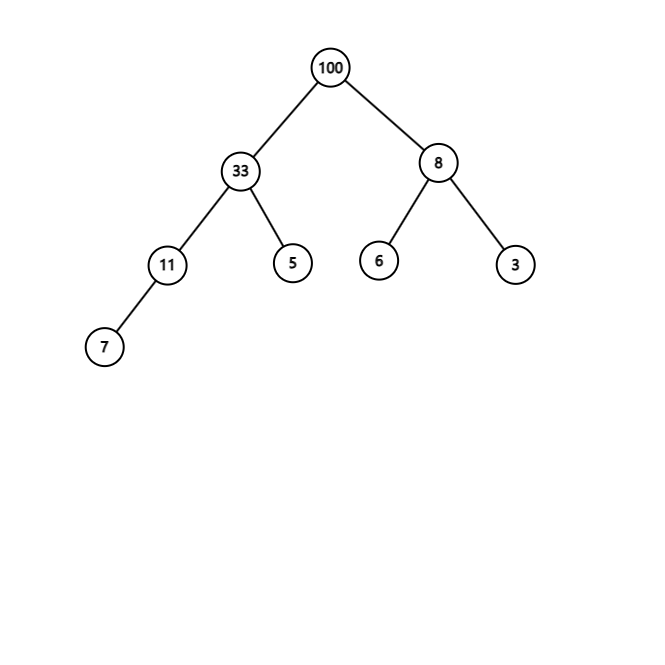
这样我们第一步就完成了,下面将整个最大堆的父节点 100 放到堆的末尾(实际上是100与7交换),我们就不管它了。
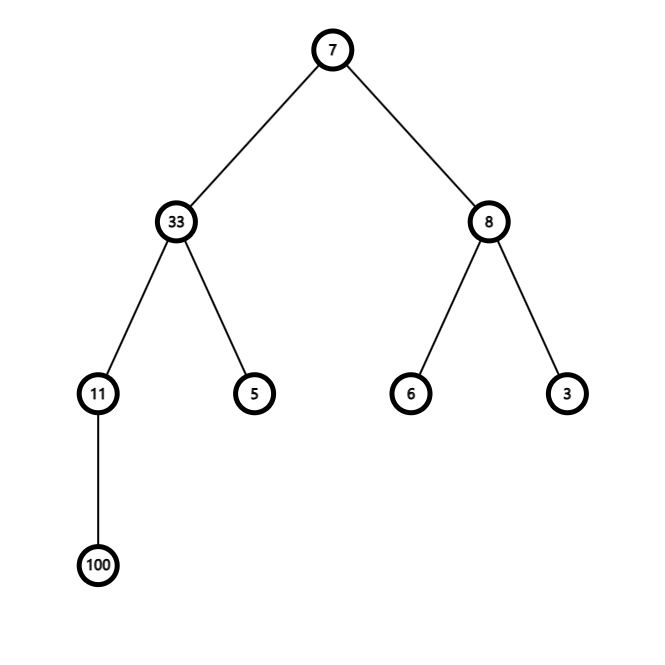
然后继续开始最大堆调整,直至一轮结束,在 7 升至顶部之后,对顶部重新做最大堆调整,左孩子33代替7的位置。这里就不给图了。
最后不断建立最大堆,并且扩大有序区,最终全部有序,最终图如下图所示
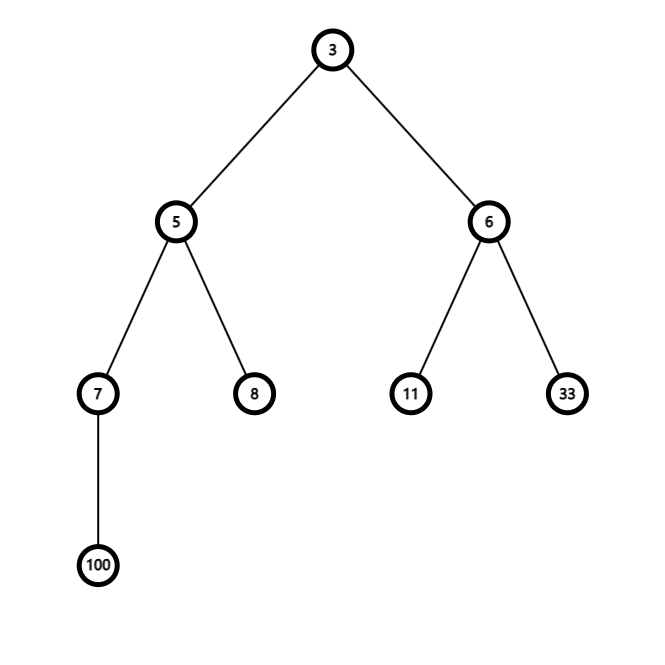
代码
1 | |
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!