并查集

并查集

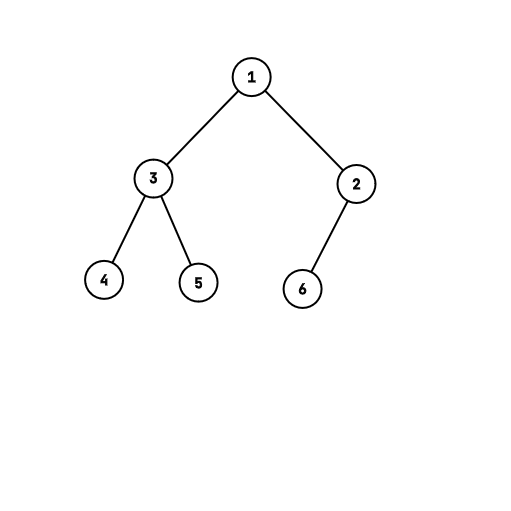
并查集是一种树形的数据结构，可以很高效的解决一些问题。

操作

有三个操作：

• 初始化
• 查找
• 合并

初始化

初始时，每个点都是自己的父亲。

int fa[maxn];
for(int i = 1;i <= n;i ++)
    fa[i] = i;

查找

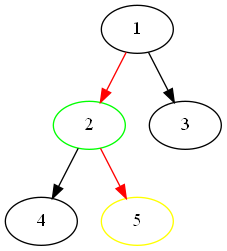
上图中，想要找 \(5\) 的祖先，先通过 \(2-5\) 这条边找到 \(2\) ，通过同样的办法找到祖先 \(1\)，\(1\) 没有祖先就得到答案了。
就像上面一样递归找到每个点的祖先，在返回答案。

代码如下：

int find(int x){
	if(x == fa[x])		return x;
    else	return find(fa[x]);
}

合并

显而易见，就是将两个集合合并。

union

挺简单的，就直接上代码吧：

void Union(int x,int y){
	int u = find(x),v = find(v);
    fa[u] = v;
}

设操作次数为 \(m\)，平均时间复杂度为 \(\mathcal{O}(m \log n)\)，最坏时间复杂度为 \(\mathcal{O}(mn)\)。

优化

在上面的操作中还是不够快，所以我们想办法优化。

路径压缩

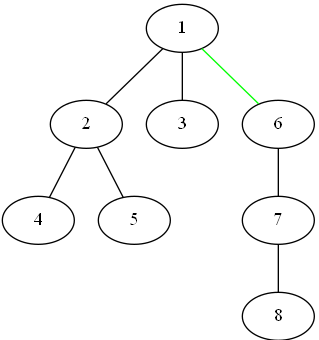
如果一个关系像一条链（如下图）一样，那么查找最下面的数的祖先的时间复杂度得退化到 \(\mathcal{O}(n)\) 。

chain

这样一层一层找太浪费时间，直接当祖先的儿子，问一次就可以出结果了。甚至祖先是谁都无所谓，只要这个人可以代表我们家族就能得到想要的效果。把在路径上的每个节点都直接连接到根上。

代码：

int find(int x){
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}

启发式合并

查找都优化了，那合并总不能不优化吧。

我们思考一个问题：如果一个点与一个含有 \(100\) 个点的集合合并，是一个点合并到 \(100\) 个点的集合快？还是 \(100\) 个点合并到一个点快？答案是显然的。
在题目中我们通常维护 点数 或 深度 来作为估价函数来合并

void Union(int x,int y){
	int u = find(x),v = find(y);
    if(u == v) return;
    if(sz[u] > sz[v])
        swap(u，v);
    fa[u] = v;
    sz[v] += sz[u];
}

优化后的时间复杂度

• 只使用路径压缩的平均时间复杂度为 \(\mathcal{O}(m \alpha(n))\)，最坏时间复杂度为 \(\mathcal{O}(m \log n)\)
• 只使用启发式合并的平均时间复杂度为 \(\mathcal{O}(m \log n)\)，最坏时间复杂度为 \(\mathcal{O}(m \log n)\)。
• 路径压缩 + 启发式合并的平均时间复杂度为 \(\mathcal{O}(m \alpha(n))\)，最坏时间复杂度为 \(\mathcal{O}(m \alpha(n))\)。

这里 \(\alpha(n)\) 表示阿克曼函数的反函数增长很慢，可以认为是常数(具体在这)。

应用

带权并查集

我们可以在并查集上维护一些东西，比如元素和，元素个数。

比如说Almost Union-Find这道题。它就是在并查集上维护一个元素和与元素个数，唯一不同的是这道题要一个虚点并查集，防止在第二个操作中下面的元素一起移动。

核心代码：

// 初始化

for(int i=1;i<=n;i++)
	 fa[i] = n+i;
        
for(int i=n+1;i<=n+n;i++)
	fa[i] = i,sz[i] = 1,sum[i] = i-n;

// 第二个操作，仅仅将一个节点移动到另一个集合上。

int u = find(x),v = find(y);
if(u != v){
	fa[x] = v;
	sz[u] --;sz[v] ++;
	sum[u] -= x;sum[v] += x;
}