最小生成树(模板)

题目

这是个模板题 链接:P3366 【模板】最小生成树 ## 题目描述 如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 $ N,M $ ，表示该图共有 $ N $ 个结点和 $ M $ 条无向边。 接下来 $ M $ 行每行包含三个整数 $ X_i,Y_i,Z_i $ ,示有一条长度为 $ Z_i $ 的无向边连接结点 $ X_i,Y_i $。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

数据规模

对于 20% 的数据，$ N≤5，M≤20 $ 。

对于 40% 的数据，$ N≤50，M≤2500 $ 。

对于 70% 的数据，$ N≤500，M≤10 $ 。

对于 100%100% 的数据：$ 50001≤N≤5000， 1≤M≤2×10^5 $ 。

题解

Kruskal 算法的主要思路： 1. 先以边的权值来给边排序，从小到大

dis0
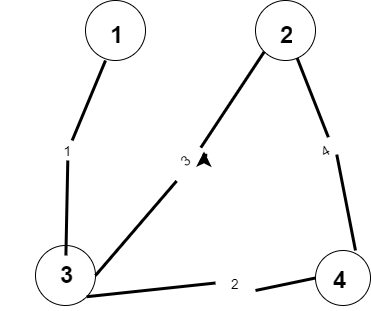
  1. 然后开始由小到大遍历边，也就是一步一步的点的扩展
dis1
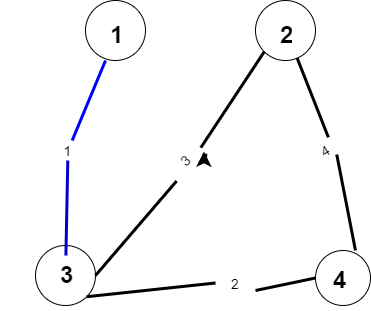
  1. 然后判断这个点的是否在已拓展的点内，如果不在就将答案加上它的边权，并且加入并查集
dis2
dis3
dis4

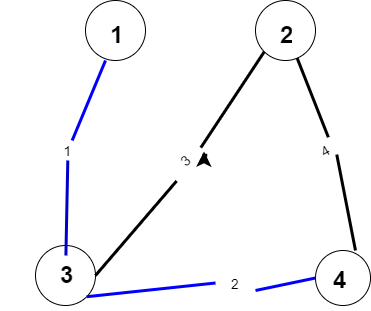
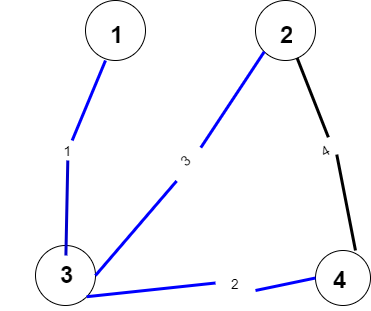
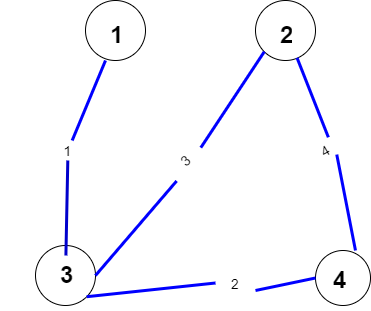
注意一下，这个是用邻接表edge写的（u，v为边的两个点，为边权），没有用领接矩阵

基本上这个模板就这样了，代码如下：

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

struct edge{ 
	int u,v,w;    //定义一个边的结构体，u、v为边的两个定点，w为边的边权
};



edge e[200005];
int father[5005];      //并查集
int ans = 0;

bool cmp(const edge& a,const edge& b){
	return a.w < b.w;        //sort（）的判断，以边权的由大到小的顺序来排序 
}

int found(int x){          //并查集的寻找父亲
	return father[x] == x ? x : father[x] = found(father[x]);        //压行，并且压缩路径，这样可以将之后的查找时间变为常数级
}

int main()
{
	int n,m;

	cin>>n>>m;

	for(int i = 1;i <= m;i++)
	{
		scanf("%d %d %d",&e[i].u,&e[i].v,&e[i].w);
	}

	sort(e,e+m,cmp);    //kruskal 算法的重要部分：按照边权的大小来排序

	for(int j = 1;j<=n;j++)	father[j] = j;  //初始化，每一个点都是一个自己的父亲

	int k = 0;
	for(int j = 1;j<=m;j++)
	{
		if(k == n - 1)	break;
		int v = e[j].v,u = e[j].u;
		if(found(v) != found(u))        //如果没有这个边所在的点没有加入，就执行下面
		{
			k++;   //注意一点：这一句话一定要在这里写，我已经掉过坑里了
			ans += e[j].w;    //加入答案：最小生成树的总长
			
			int f = found(v),t = found(u);
			father[t] = f;          //使这个的边的这个点加入路径
		}
	}




	int cnt = 0;
	for(int i = 1;i<=n;i++)
		if(father[i] == i)
                	cnt++;
	
	
	if(cnt == 1)
		cout<<ans<<endl;
	else
		cout<<"orz"<<endl;        //如果有边不联通，就输出“orz”
	getchar();getchar();
	return 0;
}